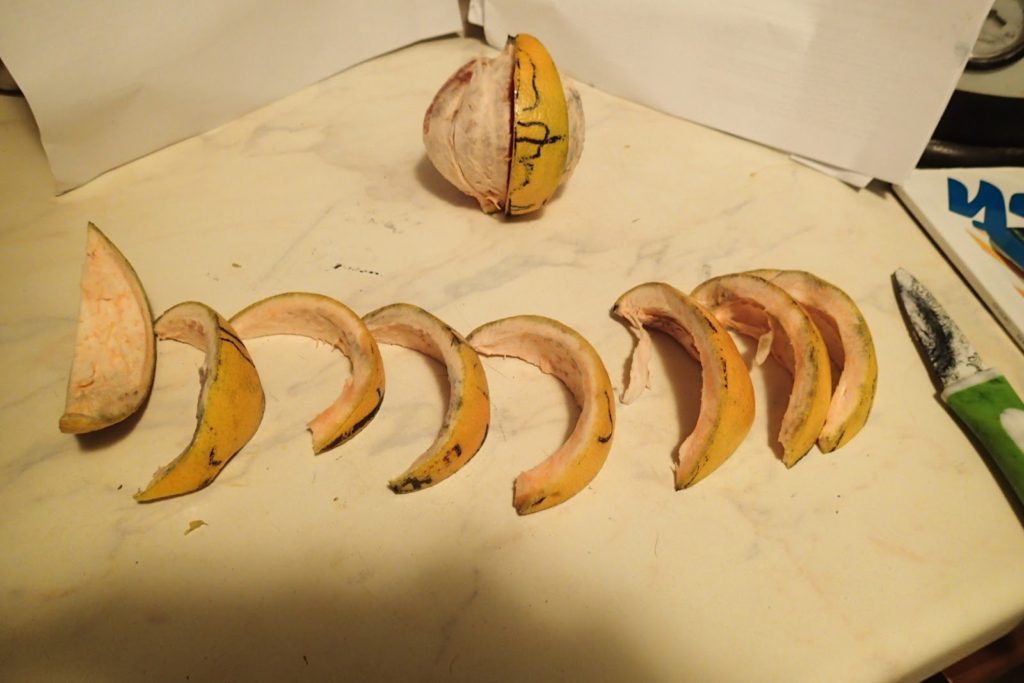Откуда берутся карты. Картографические проекции, ориентация и масштаб карт

Всем известно, что планета Земля имеет форму шара и глобус является достаточно точной моделью нашей планеты. Более продвинутые товарищи знают, что она на самом деле слегка сплющена с полюсов, а её форму называют эллипсоидом. На самом деле форма Земли сложная, неправильная, и может напоминать картошку,  и форму её называют геоидом. Про геоид мы будем говорить подробнее потом, когда мы будем рассуждать о спутниковой навигации. А пока договоримся, что Землю можно представить в виде апельсина 🙂

Раз уж я решил использовать апельсин вместо глобуса, то надо на него нанести изображение континентов. Карту привычной Земли рисовать было долго и скучно, поэтому я нарисовал на нем континенты из мира Игры престолов Дж. Мартина.

Отмечаем северный и южный полюса на нашем “глобусе”. Это точки, проткнув которые спицей, мы получим ось вращения планеты вокруг своей оси (благодаря этому вращению происходят смены дня и ночи).

___

Проводим экватор – линию равноудаленную от обоих полюсов.

Теперь у нас есть Северное и Южное полушария. И мы можем уже начать ориентироваться по нашему апельсину в направлении север-юг (верх-низ). Ведь мы можем нарисовать параллельные линии экватору – параллели и пронумеровать их как-нибудь.

Чтобы создать координаты еще и по направлению запад-восток (лево-право), надо  прочертить еще линии, соединяющие полюса – меридианы.

___

Прочертить-то мы их прочертили, но надо будет выбрать какую-нибудь одну, от которой начать считать. Это с экватором, все ясно – он линия – равноудаленная от полюсов, ровно посредине планеты (на линии север-юг), а тут надо решить творчески, какая из линий будет ровно посередине на линии запад-восток. На нашем глобусе Игры престолов я бы считал меридианы от Королевской Гавани 🙂

Глобус это хорошо, но он не всегда удобен. В карман не положишь, курс чертить сложно. Да и часто нужны масштабы покрупнее, не на весь мир хочется посмотреть, а поподробней на свой город или страну. Если опустить анекдоты про глобус Украины, то нам надо перенести картинку с глобуса (точная модель Земли без всяких искажений) на карту.

У меня не глобус, а апельсин, поэтому начну снимать с него шкурку. Разрезы буду делать аккуратненько по меридианам, чтобы потом не парится с складыванием мозаики из разорванной кожуры в карту.

___

Вот вырезал один кусочек, продолжаю.

Остался последний сегмент. Мякоть я потом съем 🙂

Все кусочки готовы к складыванию в карту.

Большинство линий континентов у меня потерлось, но суть видна… Получается какая-то фигня. Снятые с глобуса кусочки карты на плоскости в единый кусок не состыковываются!

Как ни крути:)

___

Так как же все перенести изображение на карту?

Есть много разных способов – их называют картографические проекции (проекции глобуса на карту).

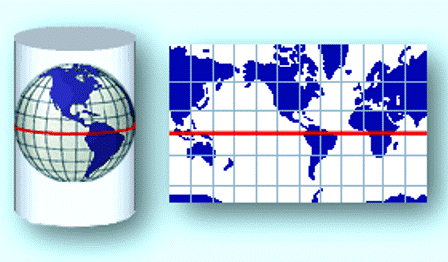
Одна из самых популярных – Равноугольная цилиндрическая проекция Меркатора. Герард Меркатор создал свою проекцию в 16 веке для нужд моряков.  До сих пор всеми используемые в интернете Яндекс и Гугл карты, карты OpenStreetMap используют эту проекцию.

Проекции со сферы на плоский лист описываются всякой сложной математикой, кому надо, тот с легкостью найдет формулы в Википедии. Нам же надо просто представить себе, что сделал Меркатор.

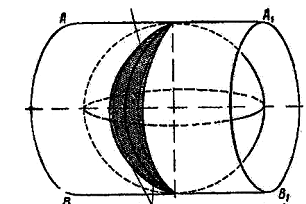
Возьмем глобус, на который сверху надели свернутый в трубочку лист бумаги. Лист будет касаться глобуса только на экваторе. А полюса будут от краев бумаги дальше всего.

А теперь представим, что меридианы на глобусе – это проволочки, а параллели – резинки (растягиваются сколько угодно). Берем проволочки и разгибаем их, пока не станут прямыми. При этом они как раз лягут на наш лист. Рисунок на глобусе был сделан из очень-очень липкой и незасыхающей краски, и, как только проволочки легли на наш лист, рисунок отпечатался на листе.

Осталось только развернуть его 🙂

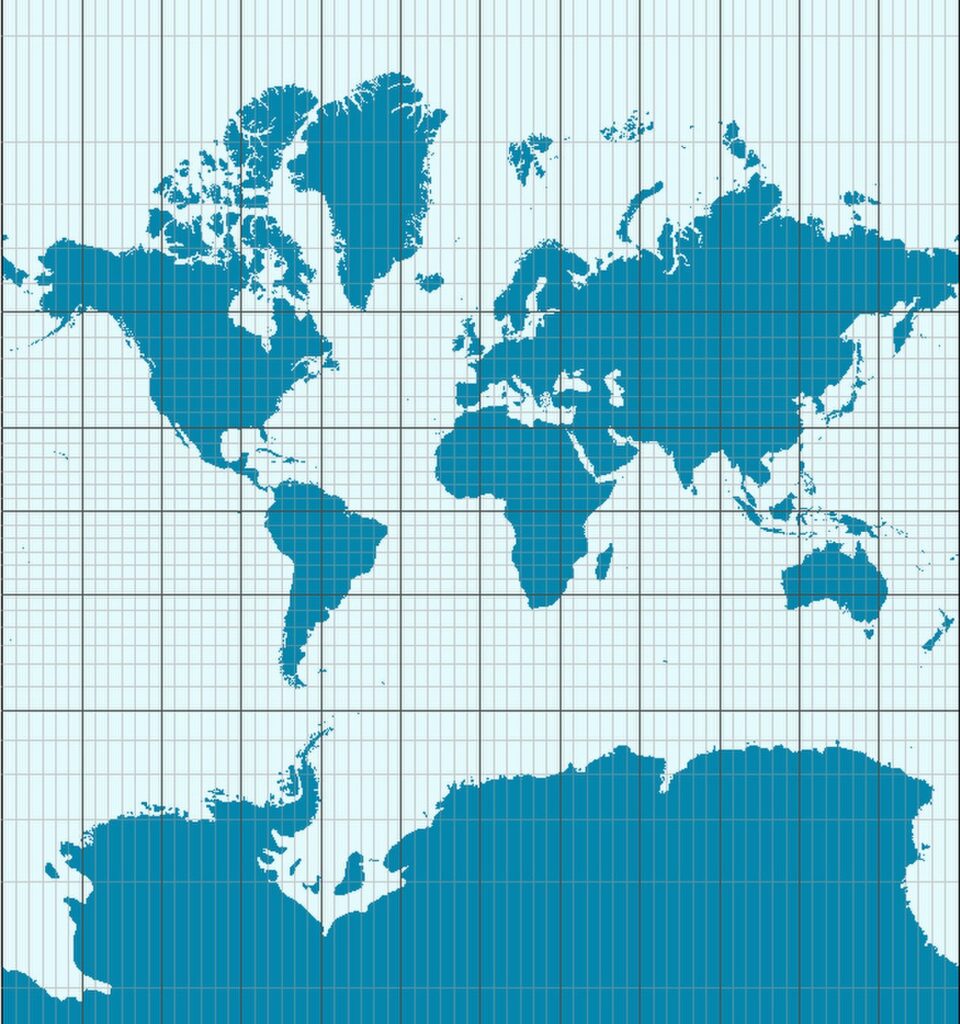
Вот что у нас получилось. Ничего не бросается в глаза странного? Посмотрите например на остров Гренландия (белый около Канады) и сравните его с материком (МАТЕРИКОМ!!!) Африка. Гренландия выглядит чуть ли не больше, если равной по размеру. А Антарктида кажется самым большим континентом на Земле, хотя мы знаем из школы, что самый большой континент – Евразия.  При этом как я сказал, эта карта используется по сей день.

Почему?

Давайте сначала посмотрим на другие проекции карт.

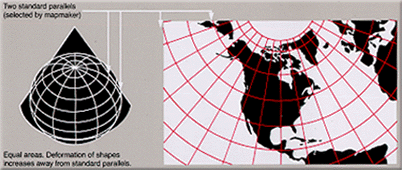
Вот например Равновеликая коническая проекция Альберса

Здесь на глобус надели конус из бумаги, а дальше все точно так же, как в меркаторской проекции. Гренландия здесь уже поместится в тот кусочек Африки, что торчит на этой маленькой карте.

Разница между этими двумя проекциями в том, что у проекции меркатора все меридианы параллельны (северный полюс на этой карте – линия!), и его проекция сохраняет форму объектов, а  у конических проекций (их на самом деле много разных) меридианы сходятся к полюсам (или еще куда в зависимости от укуренности создателя проекции) и сохраняется масштаб объектов.

Казалось бы проекция Меркатора слишком сильно искажает реальные размеры объектов (причем не линейно, чем ближе к полюсам, тем больше искажение) и не удобна. На самом деле …..

Представим, что мы хотим перелететь из Лондона в Сиэтл. нам надо сделать это побыстрее и сэкономить топливо самолета, поэтому наш путь должен быть самым коротким. Проложить такой курс на глобусе легко. Берем нитку, одним пальцем держим ее на Лондоне, другой другой рукой тянемся к Сиэтлу и прикладываем нитку там. Программа Гугл Планета Земля прочертила мне точно такую же нитку (по Дуге большого круга, как это правильно называется).

Вот как мы полетим:

Самолет вылетит из Лондона, пролетит между Шотландией и Ирландией, потом из правого иллюминатора мы сможем увидеть берега Исландии, потом мы пролетим над ледниками Гренландии, залетим на территорию Канады, пройдем севернее Гудзонова Залива и наконец-то сядем в Сиэтле, пролетев над США совсем чуть-чуть.

А теперь проложим тот же самый курс на карте Меркаторской проекции. Разложили на нашем штурманском столике карту, взяли линейку и соединили две точки.

Следуя этому курсу, мы оставим Ирландию по правому борту, а не по левому, как в прошлом случае, Исландии и Гренландии не увидим вообще (они останутся далеко на севере), на территорию Канады мы прилетим не севернее Гудзонова залива, а над Ньюфаундлендом и долго будем лететь над территорией США, почти над границей с Канадой.

Этот путь длиннее, и самолет потратит больше топлива и времени, чтобы его проделать. Зачем же тогда Меркаторская карта нужна?

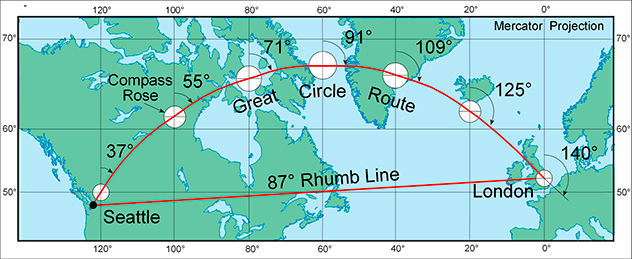
Начертим оба курса на меркаторской карте.

При движении по дуге большого круга (по кратчайшему пути), нам надо постоянно менять курс, относительно севера. И в каждой точке нашего пути пришлось бы заново считать верное направление.

Герард Меркатор создавал свою карту задолго до эпохи компьютеров и GPS для нужд моряков, не все из которых были гуру в математике, чтобы считать свой курс. А еще не было приборов, позволяющих точно  определять местоположение корабля (самолета в нашем случае) в море в любой момент. Поэтому моряки пренебрегали тем, что им придется провести чуть больше времени в море, в пользу простоты и надежности расчетов – прокладывали курс по меркаторской карте и шли всю дорогу, придерживаясь одного и того же курса относительно севера. (В нашем случае курс из Сиетла в Лондон 87 градусов).

Курс, проложенный по дуге большого круга (кратчайший в реальности путь), называют ортодромией (по гречески “прямой путь”).

Курс, выглядящий прямой только на карте меркаторской проекции, называют локсодромией (по гречески “косой путь”).

Поэтому моряки до сих пор пользуются меркаторской проекцией карт, а в электронные компьютерные карты она попала благодаря тому, что задействует небольшие вычислительные мощности компьютера при работе с ней.

Надо сказать еще об одной проекции, на которой строятся топографические карты (“генштаб” и другие). С ними часто сталкиваются туристы.

Проекция Гаусса -Крюгера (также известная как поперечно-цилиндрическая проекция Меркатора).

Представим себе что лист бумаги, свернутый в трубочку, надели на глобус не сверху, а сбоку. Тогда листа будет касаться только узкая полоска глобуса с одной стороны его и такая же ровно с противоположной

Проворачивая глобус внутри листа-цилиндра, мы так отпечатаем всю его поверхность на бумаге. Получатся такие же дольки апельсиновой шкурки, которые я резал в начале.

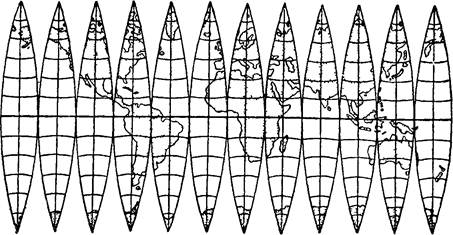
Вот как будет выглядеть карта мира в проекции Гаусса -Крюгера.

Трансокеанские плавания на такой карте вообще строить не удобно, зато, если разрезать каждую из этих долек на мелкие кусочки, то получатся достаточно точно передающие как форму (преимущество меркаторской “морской” проекции) так и размер (преимущество например конических проекций).

Посмотрите на рисунок сверху. “Дольки” уже расчерчены в клеточку параллелями и меридианами. Но представим на минуточку, что это линии по которым мы сделаем разрезы. А теперь приклеим эти мелкие кусочки на обычную бумагу, которая всегда из типографии прямоугольная.

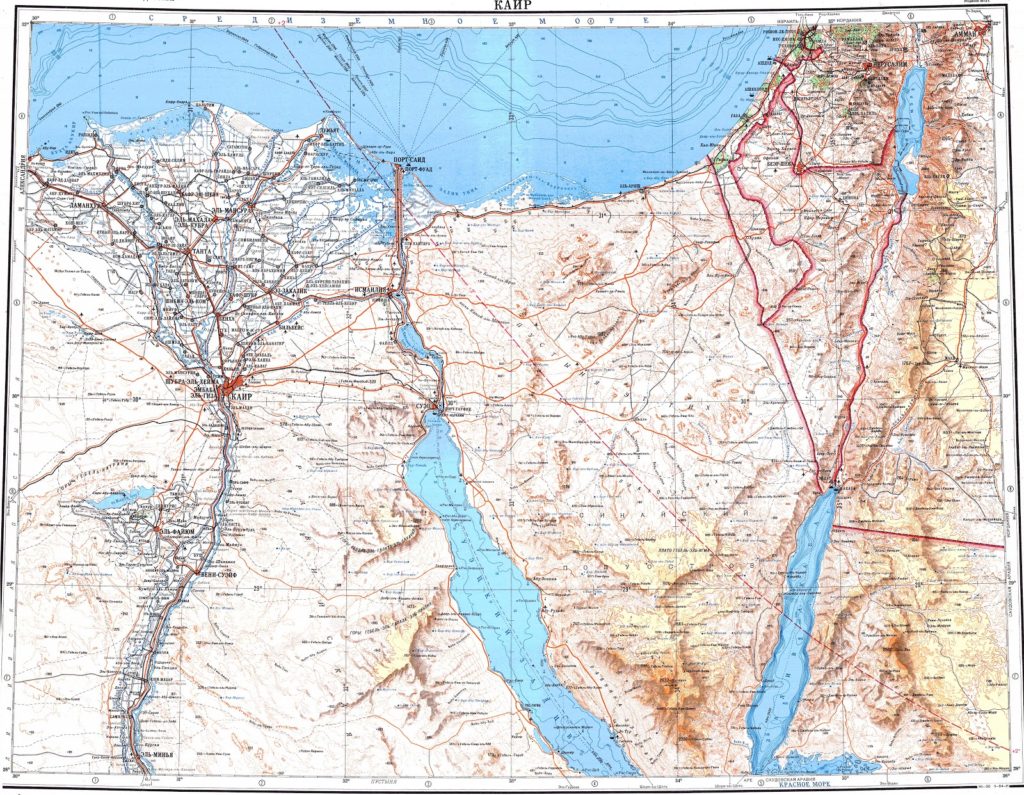
Кусочек близкий к середине, к экватору, будет почти совпадать с реальным квадратом. Вот например карта Египта

Египет и Синайский полуостров, который мы тут видим, находятся все-таки не на самом экваторе, а немного севернее и карта лишь слегка сужается к верху.

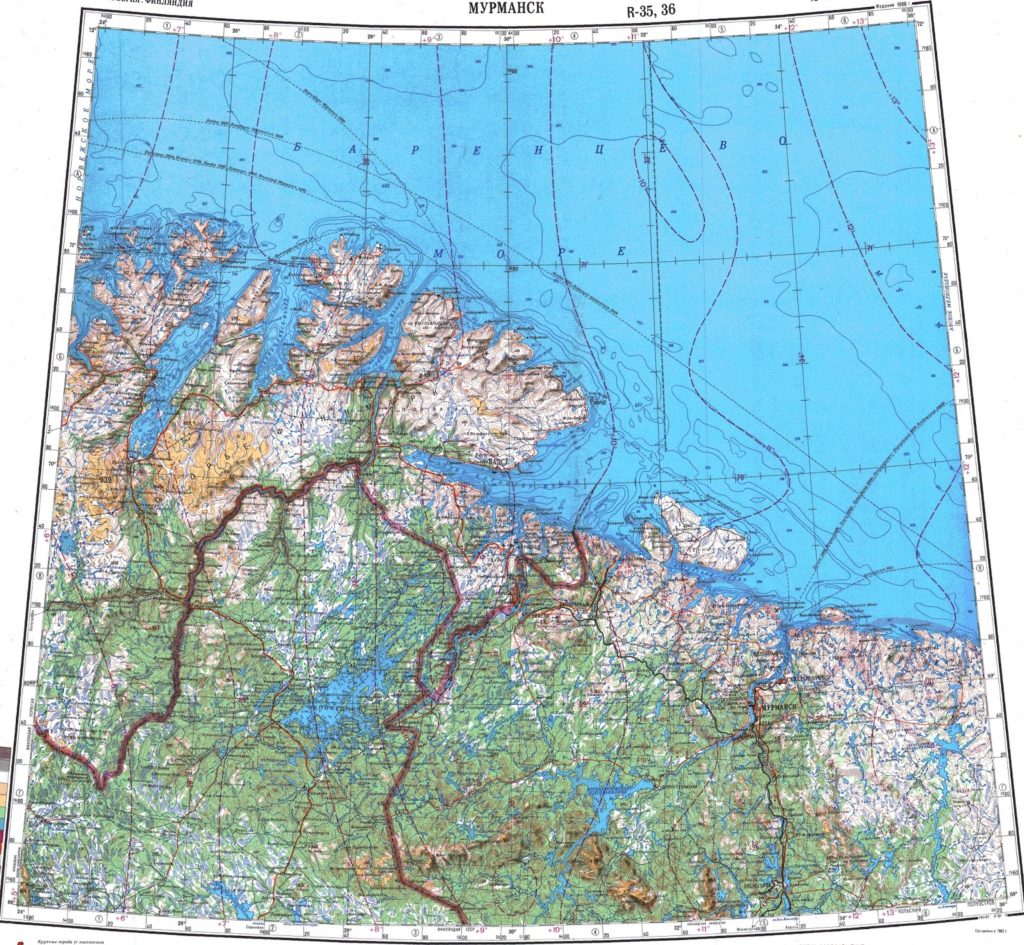
А вот карта Мурманской области, северной Финляндии и Норвегии (уже далеко на север).

Она уже совсем трапеция. Ведь она почти на самом верху “дольки”.

Топографические карты более крупного масштаба “вырезаются” уже из этих листов и на них не так будет заметна эта трапецевидность. (Подробнее о том, как это происходит, вот тут: /карты-генштаба/) Однако если вы решите склеить несколько карт, особенно из разных “долек”, у вас может не выйти ровного стыка, и не надо грешить на ножницы или кривые руки!

Ориентация карты

Когда готовая карта уже лежит перед нами и можем прочитать все слова на ней, значит у верхнего края её листа будет север. Так делают все уже последние лет 500.  В мире существует два типа карт, которые ориентированы НЕ на север:

• средневековые карты ориентированные на разные религиозные святыни (Иерусалим, Мекку, у кого что);
• карты поверхности в московском метрополитене (мне кто-нибудь объяснит, почему у них север всегда с разных сторон?!).

Вот вы уже знаете, где у карты север и как ее держать. Это уже полдела!

Масштаб

Масштаб – это на сколько реальную поверхность Земли “сжали”, чтобы она поместилась на нашем листе бумаги.

Можно встретить запись масштаба в таком виде: “1: 100 000”. Это означает, что один километр сжали в сто тысяч раз, и он стал одним сантиметром на карте. Мне кажется, это извращенская форма записи для гиков-математиков, любящих считать в уме.

Слава богу рядом обычно размещается запись “В 1 см 1 км”. Это уже куда понятнее. А на всех электронных картах, масштаб которых мы меняем, быстро нажимая всякие + и – на краю экрана или крутя колесико мышки, всегда имеется спасительная линеечка, рядом с которой есть подпись, какое расстояние она обозначает на местности.

Вот линейка масштаба на Яндекс-картах примостилась в нижнем правом углу.

Вот же она опять, когда я еще слегка “приблизил” карту.

Теперь вы узнали откуда берутся карты, куда они ориентированы и как понять на сколько они уменьшают отображаемый ими мир!  Хорошее начало для будущего картографа:)

В следующей части статей по картографии и навигации я тоже буду разукрашивать какой-нибудь фрукт, а потом расскажу подробнее о картах для походов, cпутниковой навигации и с какой стороны искать мох в лесу, если вы заблудились и решили посмотреть на мох, потому что он красивый и успокаивает:)

P:S:  На самом деле я вас обманул. Это был не апельсин, а грейпфрут!

 

Присоединиться к моим походам можно через группу во Вконтакте: https://vk.com/shuriktravel. Там есть расписание планируемых мероприятий, но проще вступить в группу, и тогда вам будут приходить приглашения в походы (у вас же стоит разрешение на приглашения на мероприятия в настройках?) 🙂